深度學習Warm up策略在幹什麼?

在梯度下降法介紹有說過適當的learning rate可以幫助找解，雖然有ADAM或是其他最佳化的方法提出，但仍有許有研究依舊採用SGD(Momentum)訓練，而且採用固定間隔下降學習率的方法，也就是一開始採用大一點的學習率來訓練模型，慢慢的在降低學習率。

採用pytroch function畫出不同epoch下的學習率的變化。黑色線: torch.optim.lr_scheduler.LambdaLR、藍色線: torch.optim.lr_scheduler.StepLR、紅色線: torch.optim.lr_scheduler.MultiStepLR

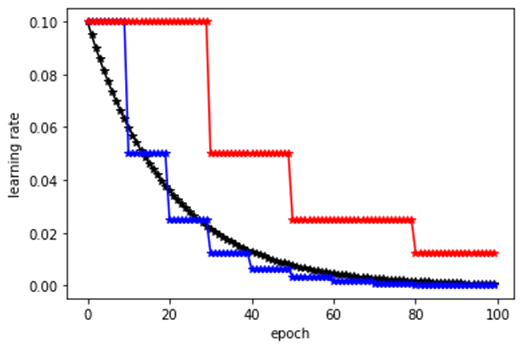
這邊先破題，warm-up機制和上述的通用法有點牴觸，warm-up需要再訓練初期使用較小的學習率來啟動，如下圖粉紅色線。

warmup為粉紅色的線，warmup設定10個epoch。

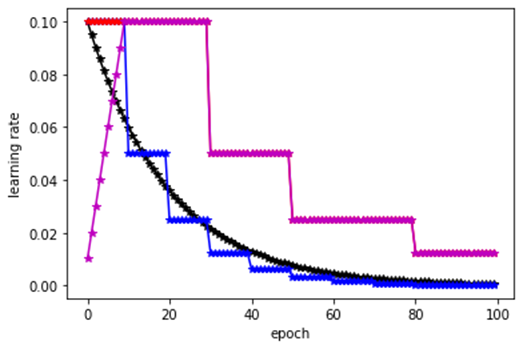
所以訓練初期可以先設定warmup的epoch數量，然後用較小的learning rate先訓練模型之後，待warmup機制結束後，在繼續一般的訓練程序。

Note: 這邊提到的warm-up為Gradual warm-up

如果只想知道warmup怎麼做，看到剛剛的圖表就可以了，後續會再針對warmup的論文進行解釋。

Gradual warm-up的機制是FB在2018年的文章 "Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour" 內提出的。但看title可以感覺出這篇文章其實應該是採用Large Mini-batch來加速ImageNet這麼大的資料庫訓練，和warmup感覺沒有關係，後續會慢慢說出為什麼需要warmup。

我們看一小段摘要原文

Specifically, we show no loss of accuracy when training with large minibatch sizes up to 8192 images. To achieve this result, we adopt a hyperparameter-free linear scaling rule for adjusting learning rates as a function of minibatch size and develop a new warmup scheme that overcomes optimization challenges early in training.

做深度學習應該知道batch size和learning rate的hyperparameter tuning對於模型訓練影響很大，因此此文章觀察不同batch size的SGD提出提出hyperparameter-free linear scaling rule調整learning rate的準則；同時他們依據hyperparameter-free linear scaling rule假設的現象，提出warmup的機制來克服訓練模型初期最佳化的問題。

所以整篇文章簡單說大概就是提出

1. hyperparameter-free linear scaling rule

2. Warmup

I. Linear Scaling Rule

文章稱這樣的策略為

Linear Scaling Rule: When the minibatch size is multiplied by k, multiply the learning rate by k。

目的是希望用較大的mini-batch取代小的mini-batch，較大的mini-batch可以加速訓練時間，但同時能要保持偵測的正確率。但見下圖，

論文節錄

上圖清楚顯示top-1 error和minibatch size的關係，文章提出的方法，當minibatch size達到8k時候，錯誤率和batch size為256時候差不多。他們採用learning rate scaling rule用256 GPUs訓練ResNet-50每個batch size = 8192，只需要1個小時即可完成訓練。

learning rate scaling rule主要是依據不同的batch size可以調整不同batch size應該採用的learning rate

以下我們舉個例子說明這個Linear Scaling Rule，首先我們先看一下當mini-batch為64個資料和640筆資料的差異，當我們用mini-batch用64個資料則10次64筆資料的更新，即可以完成640筆的資料更新，而當mini-batch用640個資料則1次更新即可完成640筆資料。我們觀察一下「10次64筆資料的更新」和「 1次640筆資料」的SGD為何?

64筆資料的SGD

640筆資料的SGD

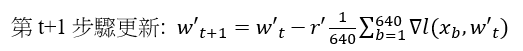
64筆資料的SGD要更新到第十次才能完成64*10=640筆資料的SGD，而640筆資料的SGD只需要一次更新就可以完成這640筆資料的SGD。

我們觀察一下

所以可以觀察到一個現象，若我們假設當

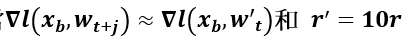
Mini-batch: 10次64筆的更新梯度= Mini-batch: 640筆的一次更新梯度

所以可以發現當batch size加大的時候，learning rate可以大一點，也就是說當我們在mini-batch size為64筆時候設定的learning rate為0.01可以訓練好模型，這時候如果我們將mini-batch size加大為640時候，我們learning rate調整為為0.01*10=0.1即可，這就是learning rate scaling rule。

論文實驗過程用的mini-batch為256時，learning rate設定為0.1，當mini-batch為8192(256*32)時，learning rate設定為0.1*32=3.2。

II Warm-up

前面就介紹完了learning rate scaling rule，那warm-up在幹什麼?

我們稍微回顧一下learning rate scaling rule有什麼重要假設

這代表mini-batch size為64筆和mini-batch size為640筆的梯度要差不多(loss不能太大)，上述的learning rate scaling rule才會成立。

但這項條件不可能永遠成立

文章有提到

for large minibatches (e.g., 8k) the linear scaling rule breaks down when the network is changing rapidly, which commonly occurs in early stages of training. We find that this issue can be alleviated by a properly designed warmup [16], namely, a strategy of using less aggressive learning rates at the start of training.

簡單說就是在一開始訓練模型的時候，模型權重的梯度(或是loss)較不穩定。

有訓練過深度學習模型的讀者應該有發現一開始的loss通常都比較大，然後在慢慢收斂。因為在模型一開始訓練的初始值為隨機生成(可參考weight initialization)的，模型對於訓練資料分布的理解度為零，因此第一個epoch的每次模型更新的時候，每筆資料對於模型來說都是全新的，基本上loss都很大。第一個epoch通常每筆資料都伴隨著有較大的loss(相對就是較大的梯度)，因此較大的梯度使得模型權重每次改變都較大，這樣就容易讓學習一開始就往該筆資料的分佈方向修正，可能導致此筆資料的overfitting，後續要靠data random shuffle和多次訓練才能將資料分布拉回來。

例如: 在第一次更新模型時，learning rate用r =0.1。當mini-batch為64更新十次的梯度為10, 9, 8, 7, 6, 5, 4, 3, 2, 1 (假設越訓練loss越小)，假設在10次更新變化為1, 0.9, 0.8, …, 0.1，如下

當mini-batch為640筆更新第一次梯度和mini-batch為64的第一個batch一樣也為10，

當mini-batch為64筆的權重更新為：1, 0.9, 0.8, …, 0.1，當mini-batch為640筆的權重更新為：1。因此learning rate scaling rule的假設不成立。

如果有個機制，模型可以針對每個資料都看過幾遍後在開始訓練，這樣每筆資料對於模型已經有了一些正確的先驗知識，但又不完全偏向某些資料，之後在進行模型訓練效果應該會更好。所以warm-up的機制一開始用小一點的learning rate，這樣模型可以看過所有資料，雖然一開始loss很大，但因為較低的learning rate這樣模型又不會更新太多。

例如: 在第一次更新模型時，learning rate調整為r =0.01。learning rate降低，因此理論上loss應該不會下降太快，且梯度不應該變化太大，所以當mini-batch為64前十次更新的梯度為10, 9.9, 9.8, 9.7, 9.6, 9.5, 9.4, 9.3, 9.2, 9.1 (假設越訓練loss越小)，乘上learning rate (r=0.01)後10次更新變化為0.1, 0.099, 0.098, …, 0.091。 當mini-batch為640筆，第一筆梯度為10，乘上learning rate (r=0.01)後權重更新變化為0.1。雖然梯度在兩個不同batch size的變化還是不同，但因為learning rate降低，更新變化已經非常接近(0.1≈0.099≈…≈0.091)。因此這樣的較低的learning rate更新方式比較不會造成劇烈梯度變化的影響，讓large mini-batch size可以順序運作。

在此這篇研究團隊還針對ResNet提出的Constant warmup機制進行測試，他們發現當給定很大的mini-batch size後，Constant warmup無法解決訓練前期最佳化的問題，因為Constant warmup較低的learning rate的過渡期結束，忽然回到較大的learning rate，讓原本會發生的問題依舊存在。因此他們提出循序漸進的warmup方式增加learning rate (Gradual warm-up)，從低的learning rate開始訓練每個epoch減緩增加一些learning rate，文章提到這樣的機制可以避免忽然的learning rate加大，使得訓練初期能有較好的收斂行為(This ramp avoids a sudden increase of the learning rate, allowing healthy convergence at the start of training)。

下圖為作者針對large mini-batch size進行的實驗，沒有warm-up 、Constant warm-up和Gradual warm-up的結果，從下圖可以發現Gradual warm-up有較合適的結果。

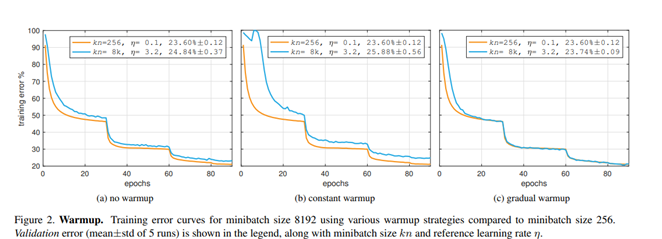
warmup結束(幾次低學習率的epoch學習結束)，模型通常比較穩定，也就是權重的分布相對較穩定，梯度通常幾次epoch後也不太會有較大的值，這時候回到正常設定的learning rate開始訓練，Linear Scaling Rule的假設通常就滿足了，梯度因為warm-up已經較低了，所以learning rate增加，梯度也不容易發生crash的狀況。

不負責任聲明: 我沒有實際做過實驗測試或是想到合理的理論基礎，因為多論文都有warm-up機制，當初只是為了探索為什麼要做 warm-up的想法，內容僅供參考。

下列程式碼是文章一開始的圖產生程式warm-up是以MultiStepLR為範例撰寫。

import math
import matplotlib.pyplot as plt
import torch
from torch import nn
import numpy as np

max_num_epochs = 100
lr_milestones = [30, 50, 80]
lr = 0.1
gamma = 0.5;

class myModel(nn.Module):
    def __init__(self):
        super(myModel, self).__init__()
        self.conv = nn.Conv2d(1, 1, kernel_size=3, stride=2, padding=1, bias=False)

    def forward(self, x):
        x = self.conv(x)
        return x


model1 = myModel()
model2 = myModel()
model3 = myModel()
optimizer1 = torch.optim.SGD(model1.parameters(), lr=lr, momentum=0.9)
optimizer2 = torch.optim.SGD(model2.parameters(), lr=lr, momentum=0.9)
optimizer3 = torch.optim.SGD(model3.parameters(), lr=lr, momentum=0.9)

lambda1 = lambda epoch: 0.95 ** epoch
scheduler1 = torch.optim.lr_scheduler.LambdaLR(optimizer1, lr_lambda=[lambda1])
scheduler2 = torch.optim.lr_scheduler.StepLR(optimizer2, step_size=10, gamma=gamma)
scheduler3 = torch.optim.lr_scheduler.MultiStepLR(optimizer3, milestones=lr_milestones, gamma=gamma)
lr1, lr2, lr3 = [], [], []
for epoch in range(max_num_epochs):
    lr1.append(float(optimizer1.param_groups[0]['lr']))
    lr2.append(float(optimizer2.param_groups[0]['lr']))
    lr3.append(float(optimizer3.param_groups[0]['lr']))
    scheduler1.step()
    scheduler2.step()
    scheduler3.step()

warm_up_epochs = 5
warm_up_with_multistep_lr = lambda epoch: ((
                                                       epoch + 1) / warm_up_epochs) * lr if epoch < warm_up_epochs else gamma ** len(
    [m for m in lr_milestones if m <= epoch]) * lr
lr_warm = []
for epoch in range(max_num_epochs):
    lr_warm.append(warm_up_with_multistep_lr(epoch))

plt.plot(np.array(range(max_num_epochs)), np.array(lr1), '*-k')
plt.plot(np.array(range(max_num_epochs)), np.array(lr2), '*-b')
plt.plot(np.array(range(max_num_epochs)), np.array(lr3), '*-r')
# plt.plot(np.array( range(max_num_epochs)),np.array(lr_warm),'*-m')
plt.xlabel('epoch')
plt.ylabel('learning rate')