深度學習: Weight initialization和Batch Normalization

14 min readSep 4, 2019

--

此篇主要寫一下weight initialization對深度學習模型的影響，以及Batch normalization的出現對weight initialization的影響。

在深度學習中除了兜模型外，最重要的就是模型內的參數，也就是weight部分，每個模型開始學習前都需要有一個對應的初始值。這時候有些人會覺得初始值不就隨機給或是給0開始學就好了啊，我一開始接觸也是這麼覺得的，對於簡單的應用(目標函數是convex)/方法這個方式可能有行，但對於神經網路而言若是有一個好的初始值對於模型學習更是事半功倍，若是初始值不好或是目標函數是non-convex問題則會造成神經網路學習到不好的結果。

這篇文章會介紹

1. weight初始值是0 [20210315修改，內容錯誤]

2. Random initialization

3. Xavier initialization

4. He initialization

5. Batch Normalization

weight初始值是0

我們先探討如果weight初始值是0會發生什麼情況

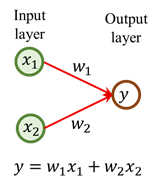
如果weight初始都是0 (w1=w2=0)

這時候forward的結果，不管你訓練資料餵什麼進模型，

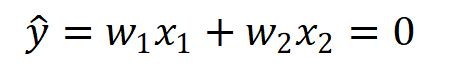
此部分的weight 初始值為0，只是輸出結果為0，假設 loss= y -y_hat=y-0=y，所以實際值(y)和輸出結果(y_hat)還是會有loss value，所以在倒傳遞的時候還是有loss往前做back-propagation。

weight初始值是0只是模型找解的出發點是從0開始更新模型，所以還是可以找解。

可以參考: "機器/深度學習-基礎數學(二):梯度下降法(gradient descent)"，初始值為0只是模型在訓練找解的過程中，一開始的出發點的差異。

Random initialization

random給予weight初始值是最常使用得方法，我們建立一個6層的MLP來看一下random initialization會產生的問題，每一層Hidden layer輸出的activation我們用tanh來處理(用sigmOid結果差不多)，然後每一層的weight都是用常態分佈生成
實驗1. 常態分佈(平均數為0，標準差為0.01)

每層Hidden輸出的直方圖。
Weight是由常態分佈隨機生成(平均數為0，標準差為0.01)。
input mean 0.00065 and std 0.99949
layer 1 mean 0.00025 and std 0.21350
layer 2 mean -0.00002 and std 0.04516
layer 3 mean -0.00001 and std 0.00899
layer 4 mean -0.00000 and std 0.00168
layer 5 mean -0.00000 and std 0.00029

實驗2. 常態分佈(平均數為0，標準差為1)

每層Hidden輸出的直方圖。
Weight是由常態分佈隨機生成(平均數為0，標準差為1)。
input mean 0.00065 and std 0.99949
layer 1 mean 0.00086 and std 0.98215
layer 2 mean -0.00057 and std 0.98082
layer 3 mean -0.00035 and std 0.97941
layer 4 mean 0.00081 and std 0.97823
layer 5 mean -0.00284 and std 0.97652

實驗3. 常態分佈(平均數為0，標準差為0.05)

每層Hidden輸出的直方圖。
Weight是由常態分佈隨機生成(平均數為0，標準差為0.05)。
input mean 0.00065 and std 0.99949
layer 1 mean -0.00155 and std 0.65968
layer 2 mean 0.00056 and std 0.51962
layer 3 mean 0.00014 and std 0.42869
layer 4 mean 0.00049 and std 0.35280
layer 5 mean -0.00005 and std 0.28212

從實驗1常態分佈(平均數為0，標準差為0.02)可以發現隨著層數的增加，每層的輸出標準差會縮小的很快(資料分布迅速往0靠攏)，後幾層基本上標準差已經接近0，神經網路的輸出值基本上很接近0，神經網路的輸出很接近0會發生什麼問題? 從weight初始值為0的結果可以得知，如果預測值接近0等於最後一層的gradient也會很小接近0，在神經網路back propagation的chain rule上最後一層的gradient接近0，後一層的gradient是前幾層的gradient的乘法係數，所以前面層的gradient也會很小，導致參數無法更新。

從實驗2常態分佈(平均數為0，標準差為1)，可以發現每層的輸出飽和了(幾乎落在-1和1附近)，這樣的gradient也都接近0，同樣的問題再次發生(每層的gradient太小)，參數無法有效被更新。

實驗3常態分佈(平均數為0，標準差為0.05)，我們可以觀察到這個時候的輸出比較是我們希望得到的，神經元的輸出結果得到有效的gradient (輸出不等於0或是極端，gradient才可以有效取得)，由這三個實驗可以發現神經網路的weight的initialization影響很大，所以需要更有效的方法設定資料的標準差。

既然weight初始值從常態分布(也可以用均勻分布)的標準差變化會造成隨機產生造成神經元輸出的結果不make sense，那是不是有什麼方法可以自動決定標準差要是多少(如果weight初始值要從均勻分布抽那就是均勻分布的上下界要怎麼設定)，所以在Xavier initialization做了很好的詮釋。

Xavier initialization

Xavier initialization為Xavier Glorot 和 Yoshua Bengio在2010年的文章《Understanding the difficulty of training deep feedforward neural networks》提出來的方法，在pytorch直接call nn.init. xavier_normal_。

上一章可以得知weight權重的生成會影響神經元的輸出太集中或是過於飽和。

Xavier論文的想法是希望神經元輸入(xi, i=1,2,…,d)和輸出(y)的變異數(variance，標準差的平方)保持一致。

這一步推導統計學有教(E是期望值)，要先懂二階動差函數的公式，然後做轉換。

然後我們假設xi和wi的平均數是0(期望值等於0)，且iid (Independent and identically distributed，獨立且同分佈，這邊有念過統計的可能比較知道在寫什麼)。

作者希望輸出的variance等於1 (Var(y)=1)

但通常我們輸入的結果會經由前一層的假設讓這層的variance=1

n_inputnode等於input node數。

同樣得程序在back-propagation也推一遍就可以得到

為了希望forward和backward的variance可以一致，文章就直接取

《Understanding the difficulty of training deep feedforward neural networks》公式12。

假設weight的生成是來自均勻分布U(a, b)且假設b = -a，這時候要生成weight的variance為(請參照統計學均勻分布變異數公式)

以上推導的activation function是我們是用linear function輸出，在一些非線性(tanh, sigmoid)也是有效的(如實驗一)，但在目前常用的ReLU上則還是有些問題(實驗二)，實驗二的輸出會隨著層數越多越後面的神經元輸出會越集中於0導致無法有效學習。

實驗一: 用Xavier initialization，神經網路activation function採用tanh輸出。

每層Hidden輸出的直方圖。
Weight是由均勻分布隨機生成(Xavier initialization)。
input mean 0.00065 and std 0.99949
layer 1 mean 0.00072 and std 0.63520
layer 2 mean -0.00023 and std 0.49814
layer 3 mean -0.00048 and std 0.42458
layer 4 mean -0.00014 and std 0.37927
layer 5 mean 0.00027 and std 0.34927

實驗二: 用Xavier initialization，神經網路activation function採用ReLU輸出。

每層Hidden輸出的直方圖。
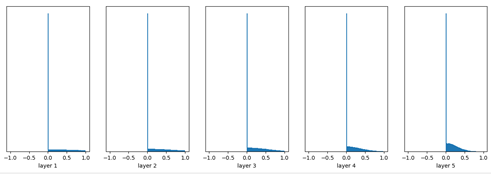
Weight是由均勻分布隨機生成(Xavier initialization)。
input mean 0.00065 and std 0.99949
layer 1 mean 0.40986 and std 0.59949
layer 2 mean 0.28339 and std 0.42536
layer 3 mean 0.22020 and std 0.31701
layer 4 mean 0.15992 and std 0.23894
layer 5 mean 0.13443 and std 0.18587

He initialization

He initialization為何鎧明的文章Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification中提出，He為何的漢語拚音，所以用He initialization，在pytorch更直接叫nn.init.kaiming_normal_。

剛剛我們看Xavier initialization問題是在ReLU中，假設每一層剛好有一半的神經元被activate，另一半為0，所以我們依舊希望輸出的variance不變，這時候要怎麼玩哩。我們從剛剛Xavier initialization的推導來看

因為He initialization的推導稍微複雜一點，需要引入前層和當層的關係，所以我將公式修改成

因為wl-1是對稱於0的分佈，所以yl-1的結果也是對稱於0的分佈(平均數等於0)，然後activation function是ReLU，所以

照這樣的推理，我們可以將此公式繼續將第L層的variance往前推到第1層

所以Var(yL)是從第一層的weight variance不斷連乘到第L層的weight variance，只要這個variance大於1或是小於1都會因為層數增加造成vanish或是explosion，所以最好的方式是希望

如果我們假設weight需要服從常態分佈平均數為0，則標準差就是

如果我們假設weight需要服從均勻分布U(a, b)且假設b = -a，這時候要生成weight的variance為(請參照統計學均勻分布變異數公式)

實驗: 剛剛 Xavier initialization發生問題的例子，改用He initialization，神經網路activation function採用ReLU輸出。

每層Hidden輸出的直方圖。
Weight是由常態分佈隨機生成(He initialization)。
input mean 0.00065 and std 0.99949
layer 1 mean 0.59251 and std 0.86758
layer 2 mean 0.63703 and std 0.91839
layer 3 mean 0.64056 and std 0.95845
layer 4 mean 0.72482 and std 1.06023
layer 5 mean 0.80317 and std 1.19583

Batch Normalization

前面說了這麼多，不外乎是要怎麼有效決定weight生成時分佈的參數，常態分佈就是決定variance，均勻分布就是決定上下界，那有沒有辦法在參數無法有效給予情況下解決問題勒，這個方法就是用Batch Normalization(BN)。BN這個方法是在Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift提出的。

有修過統計學的大概都知道z-score是什麼，在資料科學就是資料的正規化，將資料的平均數拉到0，變異數拉成1，但統計學上有假設輸入資料要是常態分佈，做z-score才會變成標準常態分佈(N(0, 1))，但在機器學習上就不要太強求資料是常態，但我們終究還是需要資料分布是常態。

BN本身就是一種方式巧妙的要解決這個問題，我們從公式來看

BN會先將資料利用資料的特性轉換到正規化空間(平均數是0，標準差是1)，然後在藉由學習的方式將資料轉換(上圖的Scale and Shift)回神經網路認為適合資料學習的空間。整個運作有點暴力法的感覺，強制將輸出拉成平均數是0，標準差是1，這時候的輸出variance就強制是1了，這時候在讓模型從資料自己學他該有的分佈情形，所以不管你參數怎麼設定結果都會因為BN變的更合適(實驗1和2)。

實驗1. Weight是由常態分佈隨機生成(平均數為0，標準差為0.01)。